Python Data Structures——Graph
08 Sep 2014 Python Data StructureDefinitions
- Vertex(node): “key”;also have additional information——”payload”
- Edge(arc): if the edges in a graph are all one-way, it’s a directed graph
- Weight
- Path
- Cycle: a path that starts and ends at the same vertex; a graph with no cycles is called an acyclic graph
Two Implementations of a Graph
adjacency matrix
Use a two-dimensional matrix.
Advantage: Simple; easy to see which nodes are connected to other nodes for small graph
Disadvantage: not efficient to store “sparse” data in matrix

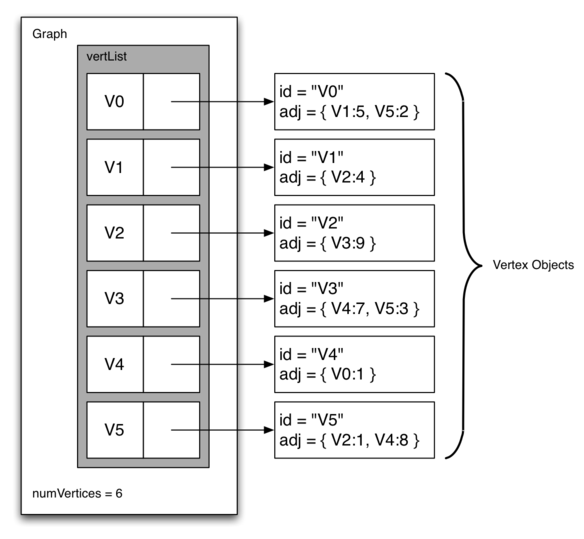
adjacency list
A more space-efficient way to implement a sparsely connected graph is to use an adjacency list.
Advantage: compactly represent a sparse graph; easily find all the links that are directly connected to a particular vertex
The Graph ADT
Graph()creates a new, empty graph.addVertex(vert)adds an instance ofVertexto the graph.addEdge(fromVert, toVert)Adds a new, directed edge to the graph that connects two vertices.addEdge(fromVert, toVert, weight)Adds a new, weighted, directed edge to the graph that connects two vertices.getVertex(vertKey)finds the vertex in the graph namedvertKey.getVertices()returns the list of all vertices in the graph.inreturnsTruefor a statement of the formvertex in graph, if the given vertex is in the graph,Falseotherwise.
Implementation
# Use dictionary, implement with adjacency list
class Vertex:
def __init__(self, key):
self.id = key
self.distance = 0
self.predecessor = None
self.color = 'white'
self.contentedTo = {}
def addNeighbor(self, nbr, weight=0):
self.contentedTo[nbr] = weight
def __str__(self):
return str(self.id) + ' contentedTo: ' + str([x.id for x in self.contentedTo])
def getConnections(self):
return self.contentedTo.keys()
def getId(self):
return self.id
def getWeight(self):
return self.contentedTo[nbr]
def setDistance(self, newdistance):
self.distance = newdistance
def getDistance(self):
return self.distance
def setColor(self, newcolor):
self.color = newcolor
def getColor(self):
return self.color
def setPred(self, newpred):
self.predecessor = newpred
def getPred(self):
return self.predecessor
class Graph:
def __init__(self):
self.vertList = {}
self.numVertices = 0
def addVertex(self, key):
self.numVertices = self.numVertices + 1
newVertex = Vertex(key)
self.vertList[key] = newVertex
return newVertex
def getVertex(self, n):
if n in self.vertList:
return self.vertList[n]
else:
return None
def __contains__(self, n):
return n in self.vertList
def addEdge(self, f, t, cost=0):
if f not in self.vertList:
nv = self.addVertex(f)
if t not in self.vertList:
nv = self.addVertex(t)
self.vertList[f].addNeighbor(self.vertList[t], cost)
def getVertices(self):
return self.vertList.keys()
def __iter__(self):
return iter(self.vertList.values())
Breadth First Search
广度优先搜索仿树的层次遍历过程,借助队列的数据结构。广度优先搜索每向前走一步可能访问一批顶点,不像深度优先搜索有回退的情况,故其不是一个递归的过程。 具体步骤为:在访问起始点v之后,依次访问v的邻接点;然后再依次访问这些点(下一层)中未访问过的邻接点;直到所有顶点都被访问过为止。
Depth First Search
深度优先搜索仿树的先序遍历,使用递归思想,借助栈的数据结构。 具体步骤为:访问起始点v,若v的第一个邻接点没访问过,深度遍历此邻接点;若当前邻接点已访问过,再找v的第二个邻接点重新深度遍历。
Topological Sort 拓扑排序
Description:
- Call dfs(g) for some graph g.
- Store the vertices in a list in decreasing order of finish time.
- Return the ordered list as the result of the topological sort.
Strongly Connected Component 强连通分量
强连通图:在有向图中,每一对顶点v,w都存在一条从v到w和从w到v的路径,则称此图为强连通图。非强连通图的极大连通子图叫做强连通分量。
Describe the algorithm to compute the strongly connected components for a graph:
- Call
dfsfor the graph G to compute the finish times for each vertex. - Compute GT.
- Call
dfsfor the graph GT but in the main loop of DFS explore each vertex in decreasing order of finish time. - Each tree in the forest computed in step 3 is a strongly connected component. Output the vertex ids for each vertex in each tree in the forest to identify the component.