Python Data Structures——Tree
02 Sep 2014 Python Data Structure- 结点的度:结点拥有的子树数
- 树的度:所有结点度中的最大值
- 树的深度(高度):所有结点中的最大层次(根结点为第零层)
二叉树的性质:
- 二叉树第i层至多有2^i 个结点
- 深度为k的二叉树,至多有2^(k+1) -1个结点
- 对于任何二叉树,若度为2的结点数有n2个,则叶子结点树n0 = n2 + 1
- 具有n个结点的完全二叉树的深度为[logn]+1(2为底的对数)
- 对完全二叉树,若从上至下,从左至右编号(从0索引开始),则编号为i的结点,其左孩子编号必为2i+1,其右孩子编号必为2i+2,其双亲编号必为[ (i-1) / 2 ]
Implementation: Binary Tree
BinaryTree()creates a new instance of a binary tree.getLeftChild()returns the binary tree corresponding to the left child of the current node.getRightChild()returns the binary tree corresponding to the right child of the current node.setRootVal(val)stores the object in parameter val in the current node.- `getRootVal() returns the object stored in the current node.
insertLeft(val)creates a new binary tree and installs it as the left child of the current node.insertRight(val)creates a new binary tree and installs it as the right child of the current node.
List of Lists Representation
def BinaryTree(root):
return [root, [], []]
def insertLeft(root, newBranch):
t = root.pop(1)
if len(t) > 1:
root.insert(1, [newBranch, t, []])
else:
root.insert(1, [newBranch, [], []])
return root
def insertRight(root, newBranch):
t = root.pop(2)
if len(t) > 1:
root.insert(2, [newBranch, [], t])
else:
root.insert(2, [newBranch, [], []])
return root
def getRootVal(root):
return root[0]
def setRootVal(root, newVal):
root[0] = newVal
def getLeftChild(root):
return root[1]
def getRightChild(root):
return root[2]
Nodes and References
class BinaryTree:
def __init__(self,rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
def insertLeft(self,newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
def insertRight(self,newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self,obj):
self.key = obj
def getRootVal(self):
return self.key
def preorder(self):
print(self.key)
if self.leftChild:
self.left.preorder()
if self.rightChild:
self.right.preorder()
树的遍历(Tree Traversals)
- 先序(preorder)
- 中序(inorder)
- 后序(postorder)
def preorder(tree):
if tree:
print(tree.getRootVal())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
def inorder(tree):
if tree != None:
inorder(tree.getLeftChild())
print(tree.getRootVal())
inorder(tree.getRightChild())
def postorder(tree):
if tree != None:
postorder(tree.getLeftChild())
postorder(tree.getRightChild())
print(tree.getRootVal())
Binary Search Tree 二叉查找树
任何一个节点的key值都比它左子树上的节点的key值要大,但是比它右子树上的节点的key值要小。(中序遍历,左小右大) 节点查找,插入,删除等操作的时间复杂度都是O(n)。
Operations
Map()Create a new, empty map.put(key,val)Add a new key-value pair to the map. If the key is already in the map then replace the old value with the new value.get(key)Given a key, return the value stored in the map or None otherwise.delDelete the key-value pair from the map using a statement of the form del map[key].len()Return the number of key-value pairs stored in the map.inReturn True for a statement of the form key in map, if the given key is in the map.
Implementation
class TreeNode:
def __init__(self,key,val,left=None,right=None,parent=None,balanceFactor=0):
self.key = key
self.payload = val
self.leftChild = left
self.rightChild = right
self.parent = parent
self.balanceFactor = balanceFactor
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild == self
def isRightChild(self):
return self.parent and self.parent.rightChild == self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChildren(self):
return self.rightChild or self.leftChild
def hasBothChildren(self):
return self.rightChild and self.leftChild
def replaceNodeData(self,key,value,lc,rc):
self.key = key
self.payload = value
self.leftChild = lc
self.rightChild = rc
if self.hasLeftChild():
self.leftChild.parent = self
if self.hasRightChild():
self.rightChild.parent = self
def __iter__(self):
if self:
if self.hasLeftChild():
for elem in self.leftChild:
yield elem
yield self.key
if self.hasRightChild():
for elem in self.rightChild:
yield elem
class BinarySearchTree:
def __init__(self):
self.root = None
self.size = 0
def length(self):
return self.size
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
# insert a item
def put(self,key,val):
if self.root:
self._put(key,val,self.root)
else:
self.root = TreeNode(key,val)
self.size = self.size + 1
def _put(self,key,val,currentNode):
if key < currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key, val, parent=currentNode)
else:
if currentNode.hasRightChild():
self._put(key, val, currentNode.rightChild)
else:
currentNode.rightChild = TreeNode(key, val, parent=currentNode)
# overload the [] operator
def __setitem__(self,k,v):
self.put(k,v)
# the retrieval of a value for a given key
def get(self,key):
if self.root:
res = self._get(key,self.root)
if res:
return res.payload
else:
return None
else:
return None
def _get(self,key,currentNode):
if not currentNode:
return None
elif currentNode.key == key:
return currentNode
elif key < currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
def __getitem__(self,key):
return self.get(key)
# implement the in operation
def __contains__(self,key):
if self._get(key,self.root):
return True
else:
return False
def delete(self,key):
if self.size > 1:
nodeToRemove = self._get(key,self.root)
if nodeToRemove:
self.remove(nodeToRemove)
self.size = self.size - 1
else:
raise KeyError('Error, key not in tree')
elif self.size == 1 and self.root.key == key:
self.root = None
self.size = self.size - 1
else:
raise KeyError('Error, key not in tree')
def __delitem__(self,key):
self.delete(key)
def spliceOut(self):
if self.isLeaf():
if self.isLeftChild():
self.parent.leftChild = None
else:
self.parent.rightChild = None
elif self.hasAnyChildren():
if self.hasLeftChild():
if self.isLeftChild():
self.parent.leftChild = self.leftChild
else:
self.parent.rightChild = self.leftChild
self.leftChild.parent = self.parent
else:
if self.isLeftChild():
self.parent.leftChild = self.rightChild
else:
self.parent.rightChild = self.rightChild
self.rightChild.parent = self.parent
'''
There are three cases to consider when looking for the successor:
1. If the node has a right child, then the successor is the smallest key in the right subtree.
2. If the node has no right child and is the left child of its parent, then the parent is the successor.
3. If the node is the right child of its parent, and itself has no right child, then the successor to this node is the successor of its parent, excluding this node.
'''
def findSuccessor(self):
succ = None
if self.hasRightChild():
succ = self.rightChild.findMin()
else:
if self.parent:
if self.isLeftChild():
succ = self.parent
else:
self.parent.rightChild = None
succ = self.parent.findSuccessor()
self.parent.rightChild = self
return succ
def findMin(self):
current = self
while current.hasLeftChild():
current = current.leftChild
return current
def remove(self,currentNode):
# remove node is leaf, no children; just remove it
if currentNode.isLeaf():
if currentNode == currentNode.parent.leftChild:
currentNode.parent.leftChild = None
else:
currentNode.parent.rightChild = None
# remove node has two children; after remove, inorder no change
elif currentNode.hasBothChildren():
succ = currentNode.findSuccessor()
succ.spliceOut()
currentNode.key = succ.key
currentNode.payload = succ.payload
# remove node has only one child
else:
if currentNode.hasLeftChild():
if currentNode.isLeftChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.leftChild
elif currentNode.isRightChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.leftChild
else: # the node is root
currentNode.replaceNodeData(currentNode.leftChild.key,
currentNode.leftChild.payload,
currentNode.leftChild.leftChild,
currentNode.leftChild.rightChild)
else:
if currentNode.isLeftChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.rightChild
elif currentNode.isRightChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.rightChild
else:
currentNode.replaceNodeData(currentNode.rightChild.key,
currentNode.rightChild.payload,
currentNode.rightChild.leftChild,
currentNode.rightChild.rightChild)
AVL Tree 平衡树
balanceFactor=height(leftSubTree)−height(rightSubTree) balance factor is -1, 0, or 1
AVL树能够对查找,插入,删除操作都达到O(logn)的效率。
AVL失去平衡时,对其进行旋转使其恢复平衡。经过这些调整,中序遍历的结果不发生改变。图形描述如下图:
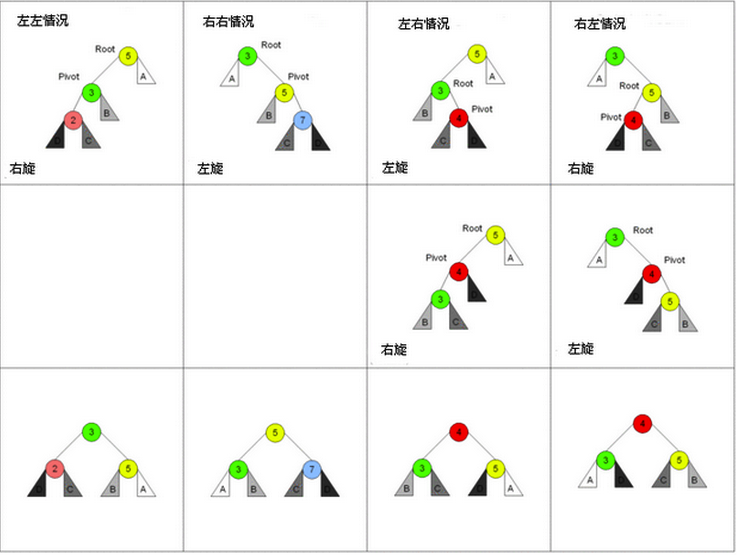
- 左旋:如果新的根节点有左孩子结点,那么左孩子结点就成为原来的根节点的右孩子结点
- 右旋:如果新的根节点有右孩子节点,那么右孩子节点就成为原来的根节点的左孩子结点
- 左右旋:先左旋,后右旋,进行两次旋转操作
- 右左旋:先右旋,后左旋,进行两次旋转操作
Implementation
# keeping an AVL tree in balance
class avlTree(BinarySearchTree):
def _put(self,key,val,currentNode):
if key < currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key,val,parent=currentNode)
self.updateBalance(currentNode.leftChild)
else:
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild)
else:
currentNode.rightChild = TreeNode(key,val,parent=currentNode)
self.updateBalance(currentNode.rightChild)
def updateBalance(self,node):
if node.balanceFactor > 1 or node.balanceFactor < -1:
self.rebalance(node)
return
if node.parent != None:
if node.isLeftChild():
node.parent.balanceFactor += 1
elif node.isRightChild():
node.parent.balanceFactor -= 1
if node.parent.balanceFactor != 0:
self.updateBalance(node.parent)
def rotateLeft(self,rotRoot):
newRoot = rotRoot.rightChild
rotRoot.rightChild = newRoot.leftChild
if newRoot.leftChild != None:
newRoot.leftChild.parent = rotRoot
newRoot.parent = rotRoot.parent
if rotRoot.isRoot():
self.root = newRoot
else:
if rotRoot.isLeftChild():
rotRoot.parent.leftChild = newRoot
else:
rotRoot.parent.rightChild = newRoot
newRoot.leftChild = rotRoot
rotRoot.parent = newRoot
rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor,0)
newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor,0)
def rotateRight(self,rotRoot):
newRoot = rotRoot.leftChild
rotRoot.leftChild = newRoot.rightChild
if newRoot.rightChild != None:
newRoot.rightChild.parent = rotRoot
newRoot.parent = rotRoot.parent
if rotRoot.isRoot():
self.root = newRoot
else:
if rotRoot.isLeftChild():
rotRoot.parent.leftChild = newRoot
else:
rotRoot.parent.rightChild = newRoot
newRoot.rightChild = rotRoot
rotRoot.parent = newRoot
rotRoot.balanceFactor = rotRoot.balanceFactor - 1 - min(newRoot.balanceFactor,0)
newRoot.balanceFactor = newRoot.balanceFactor - 1 + max(rotRoot.balanceFactor,0)
def rebalance(self,node):
if node.balanceFactor < 0:
if node.rightChild.balanceFactor > 0: # right-left rotate
self.rotateRight(node.rightChild)
self.rotateLeft(node)
else: # left rotate
self.rotateLeft(node)
elif node.balanceFactor > 0:
if node.leftChild.balanceFactor < 0: # left-right rotate
self.rotateLeft(node.leftChild)
self.rotateRight(node)
else: # right rotate
self.rotateRight(node)