JanZou analyst, programmer

Python Algoritms——Search

23 Aug 2014 Python Algorithm

本文主要总结几种基本的查找算法，线性查找法、二分查找法及哈希查找法；并给出map ADT的实现。

查找主要可分为静态查找、动态查找和哈希查找三种方式。

静态查找的主要算法有：顺序查找（线性查找）、折半查找（二分查找）、分块查找（索引顺序查找）及静态树查找。

动态查找主要是通过二叉排序树（或二叉查找树），其查找形式与折半查找类似，但采用链式存储。当二叉排序树呈现单支树（数据有序）的形态时，查找时间效率与线性查找相同，最好的情况可与折半查找一样达到O(logn)。使二叉排序树平衡可提高查找效率。具体实现细节见Tree的相关总结。

Implement

def sequential_search(a_list, item):
    pos = 0
    found = False

    while pos < len(a_list) and not found:
        if a_list[pos] == item:
            found = True
        else:
            pos = pos + 1
    return found

def ordered_sequential_search(a_list, item):
    pos = 0
    found = False
    stop = False
    while pos < len(a_list) and not found and not stop:
        if a_list[pos] == item:
            found = True
        else:
            if a_list[pos] > item:
                stop = True
            else:
                pos = pos + 1
    return found

顺序查找算法简单，对顺序结构和链表结果均适用。 顺序查找的时间效率太低，为𝑂(𝑛)。有序列表仅能在查找不成功时提高效率。

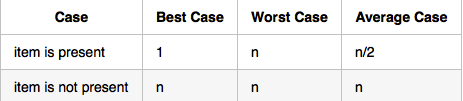
  • Analysis of The Sequential Search on common list analsis1

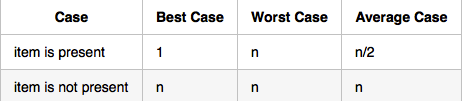
  • Analysis of The Sequential Search on ordered list analsis1

Implement

def binary_search(a_list, item):
    first = 0
    last = len(a_list) - 1
    found = False

    while first <= last and not found:
        midpoint = (first + last) // 2
        if a_list[midpoint] == item:
            found = True
        else:
            if item < a_list[midpoint]:
                last = midpoint - 1
            else:
                first = midpoint + 1
    return found


def binary_search_recursive(a_list, item):
    if len(a_list) == 0:
        return False
    else:
        midpoint = len(a_list) // 2
        if a_list[midpoint] == item:
            return True
        else:
            if item < a_list[midpoint]:
                return binary_search_recursive(a_list[:midpoint], item)
            else:
                return binary_search_recursive(a_list[midpoint+1:], item)

二分查找只适用于有序表及顺序存储结构，对数据进行全排序。 二分查找的时间效率为𝑂(log 𝑛)。

分块查找

分块查找的思路是： 先让数据分块有序，即分成若干子表，要求每个子表中的数据元素值都比后一块中的数值小（子表内不一定有序），然后将各子表中的最大关键字构成一个索引表，表中还包含每个子表的起始地址。（块间有序，块内无序） 对索引表进行折半查找，确定待查关键字所在子表后，在子表内采用顺序查找。

Hashing

Common Hash Functions

  • 除留余数法（remainder method）: 取余数
  • 折叠法（folding method）：原字符串分组求和再取模
  • 平方取中法（mid-square method）：对数字进行平方运算，然后取其中间两位数，再取模
  • ord函数：对于有字符的元素使用ord函数，将字符串转换成一个有序的数值序列。在Python中，ord函数可以得到对应字符的ASCII码值。将所有字符的码值累加再取余数（回文构词法构成的字符串得到的值总是一样的，可以根据字符的位置添加一个权重）
  • 直接寻址法：取关键码或关键码的某个线性函数值的散列地址；即hash(k)=a·k+b（a,b为常数）
  • 乘余取整法：将关键码乘以a，取其小数部分，然后再放大b倍并取整；即hash(k)=b·(a·k mod 1)(a,b为常数)
  • 数字分析法：选用关键字的某几位组合成哈希地址。（选用原则：各种符号在该位上出现的频率大致相同）
  • 随机数法：适用于长度不等的情况；hash(k) = random(k)

Collision Resolusion

  • 开放寻址法(open address）：线性探测（linear probing）下一个位置；即Hi = (Hash(key)+di) mod m (m为哈希表长度；d为增量序列1，2，……m-1，且di=i)。 缺点是容易造成聚集现象（cluster），解决聚集现象的办法是跳跃式地查找下一个空槽。
  • 平方探测法（quadratic probing）：Hi = (Hash(key)+di) mod m (m为哈希表长度，要求为某个4k+3的质数；d为增量序列1，4，9……，且di=i^2)
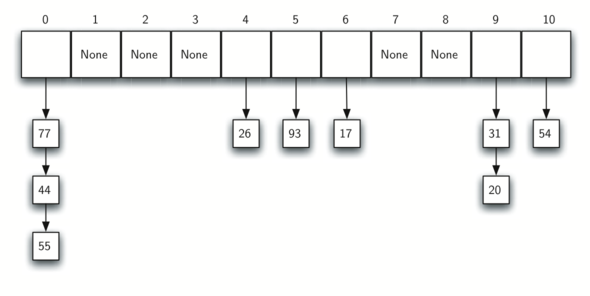
  • 链地址法（Chaining）：将具有相同哈希地址的记录链成一个单链表，用一个数组将m个单链表的表头指针存储起来。 chaining
  • 再哈希法：当产生冲突时计算另一个哈希函数，直到冲突不再发生。Hi = RHi(k)
  • 建立一个公共溢出区：一旦发生冲突，都填入溢出表

Analysis of Hashing

哈希查找的过程与哈希造表的过程基本一致。由于有冲突产生，哈希查找的过程仍然要进行比较，仍然要以平均查找长度ASL来衡量，哈希查找的时间效率并不是真正为𝑂(1)。哈希表的查找性能与载荷因子（load factor, λ）有关。

λ = number of items / table size

λ表示哈希表的装满程度。λ越大，表明填入表中的元素越多，产生冲突的可能性就越大，查找时比较次数就越多。实际上，哈希表的平均查找长度是载荷因子的函数，只是不同处理冲突的方法有不同的函数。

对于开放寻址法，荷载因子是特别重要因素，应严格限制在0.7-0.8以下。超过0.8，查表时的CPU缓存不命中（cache missing）按照指数曲线上升。因此，一些采用开放寻址法的hash库，如Java的系统库限制了荷载因子为0.75，超过此值将resize散列表。

Map ADT

we use two lists to create a HashTable class that implements the Map abstract data type.

  • Map() Create a new, empty map. It returns an empty map collection.
  • put(key,val) Add a new key-value pair to the map. If the key is already in the map then replace the old value with the new value.
  • get(key) Given a key, return the value stored in the map or None otherwise.
  • del Delete the key-value pair from the map using a statement of the form del map[key].
  • len() Return the number of key-value pairs stored in the map.
  • in Return True for a statement of the form key in map, if the given key is in the map, False otherwise.
class HashTable:
    def __init__(self):
        self.size = 11
        self.slots = [None] * self.size
        self.data = [None] * self.size

    def put(self, key, data):
        hashvalue = self.hashfunction(key, len(self.slots))

        if self.slots[hashvalue] == None:
            self.slots[hashvalue] = key
            self.data[hashvalue] = data
        else:
            if self.slots[hashvalue] == key:
                self.data[hashvalue] = data    # replace
            else:
                nextslot = self.rehash(hashvalue, len(self.slots))
                while self.slots[nextslot] != None and self.slots[nextslot] != key:
                    nextslot = self.rehash(nextslot, len(self.slots))
                if self.slots[nextslot] == None:
                    self.slots[nextslot] = key
                    self.data[nextslot] = data
                else:
                    self.data[nextslot] = data    #replace

    def hashfunction(self, key, size):
        return key % size

    def rehash(self, oldhash, size):
        return (oldhash + 1) % size

    def get(self, key):
        startslot = self.hashfunction(key, len(self.slots))

        data = None
        stop = False
        found = False
        position = startslot
        while self.slots[position] != None and not found and not stop:
            if self.slots[position] == key:
                found = True
                data = self.data[position]
            else:
                position = self.rehash(position, len(self.slots))
                if position == startslot:
                    stop = True
        return data

    def __getitem__(self, key):
        return self.get(key)

    def __setitem__(self, key.data):
        self.put(kay, data)

Related Posts